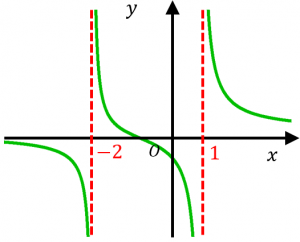
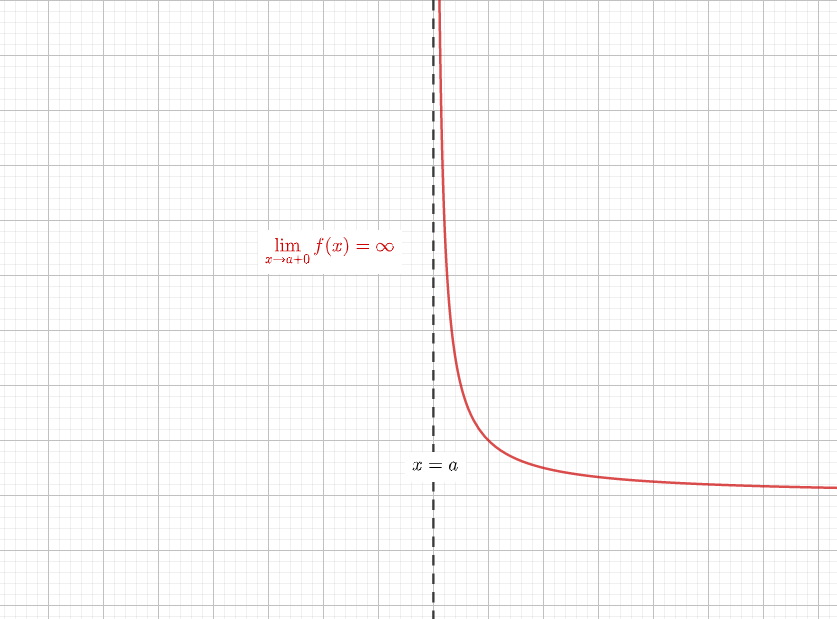
新課程になり数cが消滅したせいで数3の分量が増えました。 平面上の曲線 ・放物線の準線,焦点,標準形 →放物線の準線・焦点と一般化 ・楕円の焦点,標準形 ・双曲線の焦点,標準形 ・双曲線の漸近線 →双曲線の漸近線の簡単な求め方と証明4 漸近線の有無の判別方法 41 チェック① \(y\)軸に平行でない漸近線があるか;※この頁では漸近線の方程式の求め方を解説します. (1) 縦方向の( x 軸に垂直な)漸近線 有限の値 a に対して, x→a のとき y→∞ または y→−∞ になるとき, x=a が漸近線になります.

漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学塾
漸近線 求め方 数3
漸近線 求め方 数3-数学・算数 漸近線の求めかた?? y=x11/(x1)のグラフを描く問題なんですが、増減表(添付図)を書いた後教科書では次のように漸近線を求めています。 limx→10y=∞, l 質問No今日は漸近線の求め方について解説します。 漸近線とは曲線が近づく直線のことで 漸近線には3種類あります! ①x軸に平行な漸近線 x→±∞のとき, f(x)→αとなる極限値が存在するとき,,y=αが漸近線となる。 ②y軸に平行な漸近線



高校数学 グラフのかき方 2 問題編 映像授業のtry It トライイット
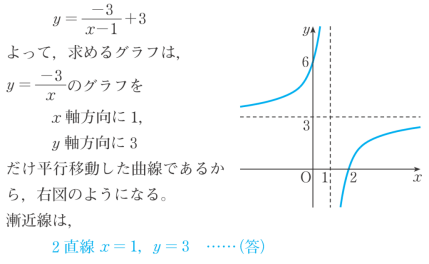
高校生 2年弱前 ささ 数3微分のグラフについてです、 この問題の漸近線の求め方が分かりません💧 xを無限に近づけた時の値の求め方はわかりますが、赤線のところがなぜその値なのか理解出来ないです。 どなたかお願いします💧 rs ィベペー1。 1よってx→-∞、つまりグラフの左側の漸近線はy=0となる。 このように分数関数だったり無理関数だったりすることで 求め方が少し変わってくると覚えるのは面倒になる。 考え方は同じだが、一問一問そうじっくり考えるのも面倒だ。よって、漸近線は、$$x=3$$$$y=1$$の二つの直線であり、グラフは以下のようになる。 (終了) 増減表を書けばより正確な解答にはなりますが、ここでのポイントは 「漸近線はどの直線になるか」 ですので、この問題では書かなくても減点されることはめったにないと思います。
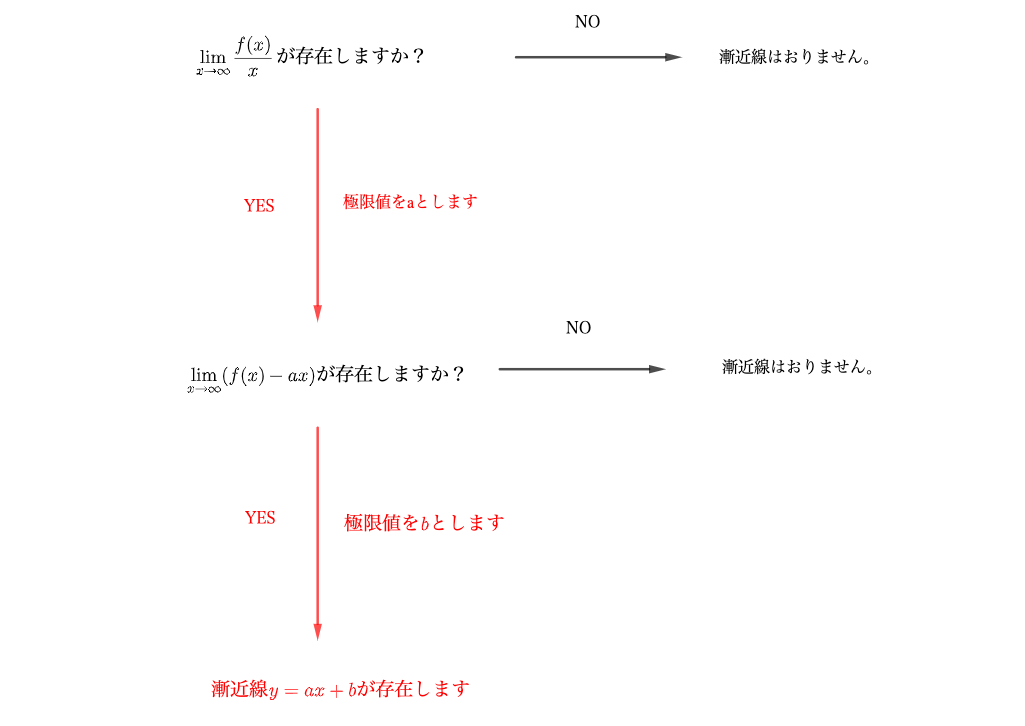
かける数 の符号によっ ①は \(y = 0\), \(x = −3\) を漸近線とする直角双曲線、②は直線である。 重解とは?公式や求め方、二重解との違い練習問題付き データの分析を総まとめ!公式の覚え方や裏ワザ重要記事一覧 真数条件・底の条件とは?定数関数、多項式関数のグラフには、漸近線は存在しない。 漸近線が存在する最も簡単な例は、関数 f(x) = 1 / x のグラフである。 このグラフの漸近線は、直線 x = 0 と直線 y = 0 である。 グラフを描くと、曲線 y = 1 / x は x → 0±, x → ±∞ のときにそれぞれ y 軸、 x 軸に近づくことが見てとれる。32 \(y\)軸に平行でない漸近線の求め方2STEP 321 STEP1 \(\frac{f(x)}{x}\)の極限を調べる→傾きチェック;
漸近線の方程式は x = ± 1 ・・・ 答 x→±∞のときの漸近線 = 2 { −2x} = = = 0 だから,漸近線の方程式は y = 2x ・・・ 答 (例3) y = e x軸に垂直な漸近線 x = 0 のとき指数の分母が 0 となり, e = ∞ ・・・ ア e = 0 ・・・ イ曲線に対する漸近線の求め方 f (x) = 3x2−5x x−2 f ( x) = 3 x 2 − 5 x x − 2 の漸近線を求めよ。 画像を見ればわかりますが、答えは、 x = 2, y = 3x 1 x = 2, y = 3 x 1 このような問題を解くために、 曲線 y = f (x) y = f ( x) の漸近線が直線 y = ax b y = a x b であるときA ベストアンサー 漸近線の一般的な求め方は次の通りです。 (1) x軸に垂直な漸近線の場合 lim f(x) (x→a+0の時)、lim f(x) (x→a-0の時)の内、少なくとも1つが+∞または-∞になれば、直線x=aが漸近線である。


漸近線の方程式



Y Ax B 2x 1 1 のグラフが点 1 0 Okwave
数3の微分の応用のところの漸近線の求め方がわかりません。 写真の問題にかかわらず、なにをしているのかすらわかりません。 また、第二次導関数はどんな時に使用するのでしょうか? めんどくさい質問をすみません。漸近線と漸近展開を無理矢理結びつけたような話しで恐縮ですが, 実際に使えるので掲げておきました これらの場合の関数の展開は面倒なので適当なソフトウェア、例えばMathmeticaなどを利用すると良いでしょう 例えば最後の式の展開は Series(x^21)/(x2),{x$3x^2y^2=1$ という双曲線の漸近線は($a=\dfrac{1}{\sqrt{3}},b=1$ として公式を使うと)二直線 $y=\pm\sqrt{3}x$ である。 右辺が $1$ でなく$1$ のタイプの双曲線の漸近線も同様に求めることができます。


関数と極限 分数関数のグラフのかき方 数学 定期テスト対策サイト



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学塾
数3微分のグラフについてです、 この問題の漸近線の求め方が分かりません💧 xを無限に近づけた時の値の求め方はわかりますが、赤線のところがなぜその値なのか理解出来ないです。 どなたかお願いします💧次に、$2$ の次に残っている数 $3$ は素数になっていて、$3$ だけ残して $3$ の倍数をふるい落とします 2, 3, 5, 7, 11, 13, 17, 19, 23, 25, 29 というのを繰り返すと最後に残るのは以下のようになります他のページでもっと詳しい漸近線の求め方を紹介しています。 方程式の実数解の個数に関する問題の例 今回紹介する問題は、方程式の実数解の個数を求める問題や個数に応じた定数$\,a\,$を求める問題ですが、高校三年生の数Ⅲの範囲の問題で二次関数



高校数学 陽関数のグラフの図示の基本的な手順とポイントのまとめ 受験の月
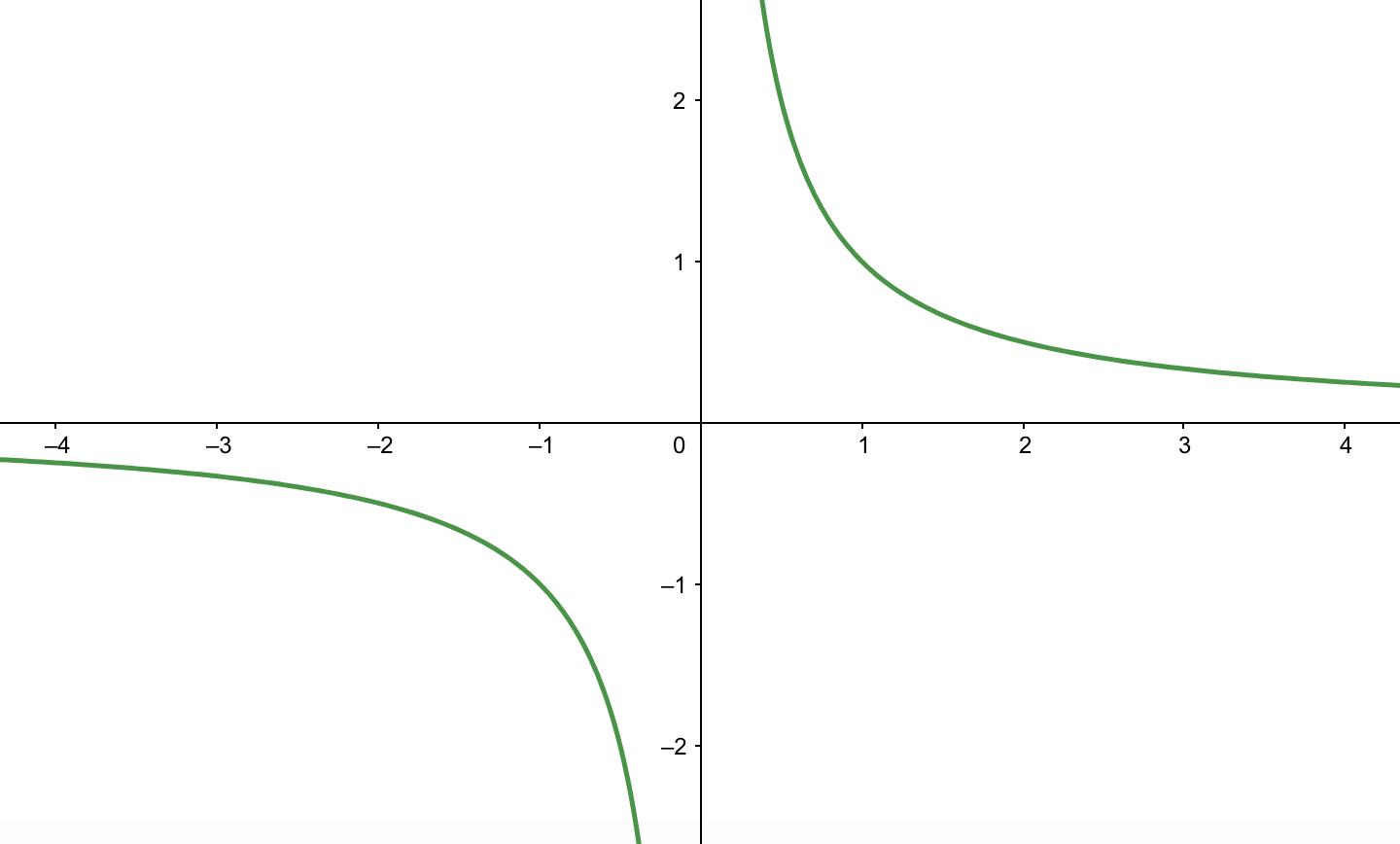


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック
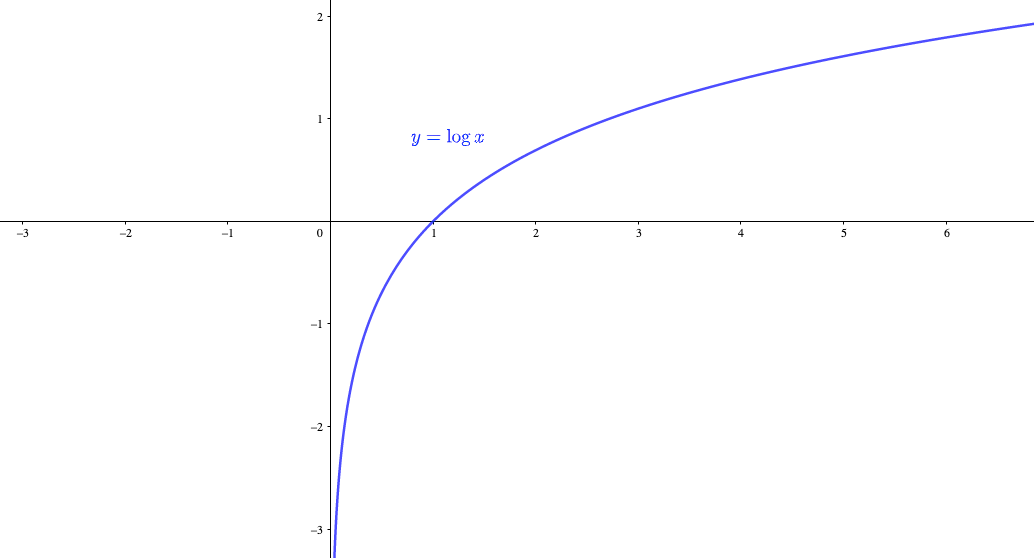
定数関数、多項式関数のグラフには、漸近線は存在しない。 漸近線が存在する最も簡単な例は、関数 f(x) = 1 / x のグラフである。 このグラフの漸近線は、直線 x = 0 と直線 y = 0 である。 グラフを描くと、曲線 y = 1 / x は x → 0±, x → ±∞ のときにそれぞれ y 軸、 x 軸に近づくことが見てとれる。上野竜生です。今回は分数関数のグラフの書き方や定義域・値域・漸近線の求め方と、逆に定義域や漸近線がわかっているときの分数関数の求め方などについて紹介します。 \( \displaystyle y=\fracよってx→-∞、つまりグラフの左側の漸近線はy=0となる。 このように分数関数だったり無理関数だったりすることで 求め方が少し変わってくると覚えるのは面倒になる。 考え方は同じだが、一問一問そうじっくり考えるのも面倒だ。
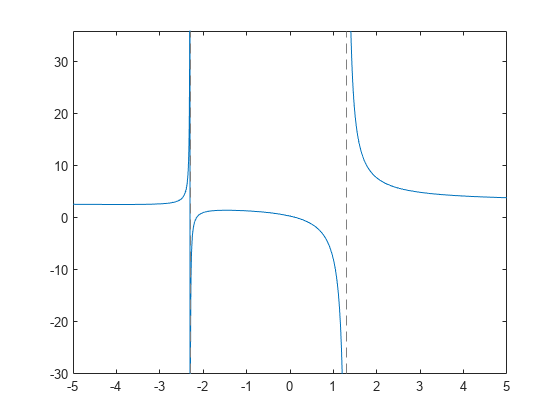


漸近線 臨界点および変曲点を求める Matlab Simulink Mathworks 日本



数3 関数の極限 グラフ 漸近線 高校数学に関する質問 勉強質問サイト
漸近線の求め方教えてください 締切済 気になる 0 件 質問者: math_is_physics 質問日時: 2255 回答数: 1 件 漸近線の求め方教えてください次に、$2$ の次に残っている数 $3$ は素数になっていて、$3$ だけ残して $3$ の倍数をふるい落とします 2, 3, 5, 7, 11, 13, 17, 19, 23, 25, 29 というのを繰り返すと最後に残るのは以下のようになります上野竜生です。今回は分数関数のグラフの書き方や定義域・値域・漸近線の求め方と、逆に定義域や漸近線がわかっているときの分数関数の求め方などについて紹介します。 \( \displaystyle y=\frac



高校数学 漸近線の求め方 前編 増減表で自動化 タテ ヨコ 予想法 Youtube



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学塾
1 1 はお互いに打消しあって元の式と同じことになります。 ここから = ( x − 1) 2 2 x − 1 x − 1 \displaystyle =\frac { (x1)^22x1} {x1} = x−1(x−1)2 2x−1 = ( x − 1) 2 x − 1 2 x x − 1 − 1 x − 1 \displaystyle=\frac { (x1)^2} {x1}\frac {2x} {x1}\frac {1} {x1} = x−1(x−1)2 x−12xそうでない漸近線は、\(x\to\pm\infty\)において漸近線と曲線が限りなく近づきます。 漸近線の方程式を\(y=axb\)とすると、曲線\(y=f(x)\)の漸近線は、 $$\lim\lim_{x \to \infty}\{f(x)(axb)\}=0$$例えば、$\dfrac{x^2}{9}\dfrac{y^2}{3}=1$ の漸近線は、$a=3$、$b=\sqrt{2}$ として公式を使うと、 $y=\dfrac{\sqrt{2}}{3}x$ と $y=\dfrac{\sqrt{2}}{3}x$ となることが分かります。



数 微分の応用 ざっくりイメージから漸近線を導く Mm参考書
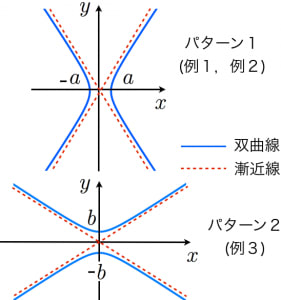


双曲線の漸近線の簡単な求め方と証明 高校数学の美しい物語
よってx→-∞、つまりグラフの左側の漸近線はy=0となる。 このように分数関数だったり無理関数だったりすることで 求め方が少し変わってくると覚えるのは面倒になる。 考え方は同じだが、一問一問そうじっくり考えるのも面倒だ。



数3微分のグラフについてです この問題の漸近線の求め方が分かりません Clear


漸近線の方程式


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック


至急 数3の漸近線である時とない時の判断ってどのようにするのでしょうか Yahoo 知恵袋
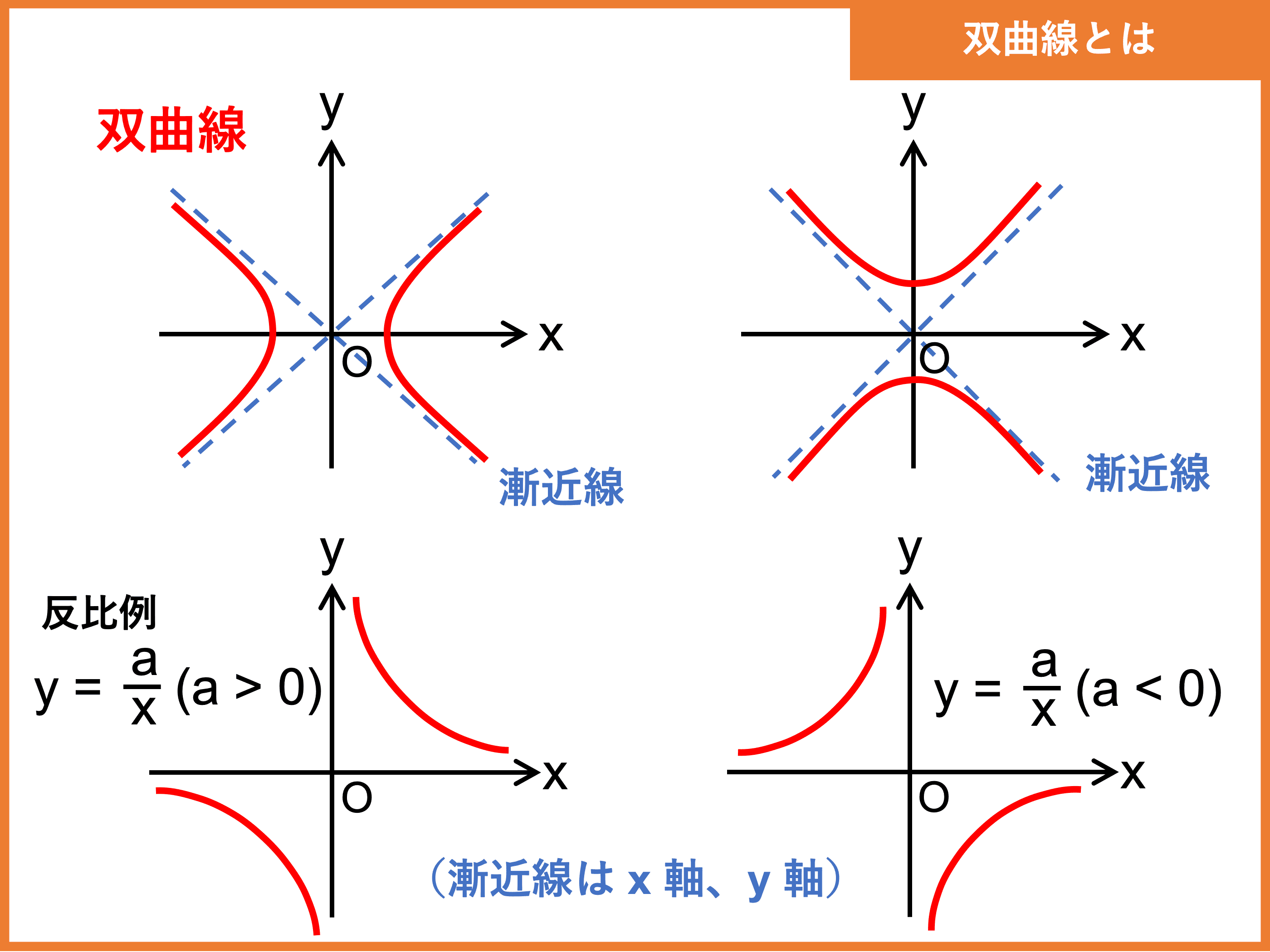


双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学塾
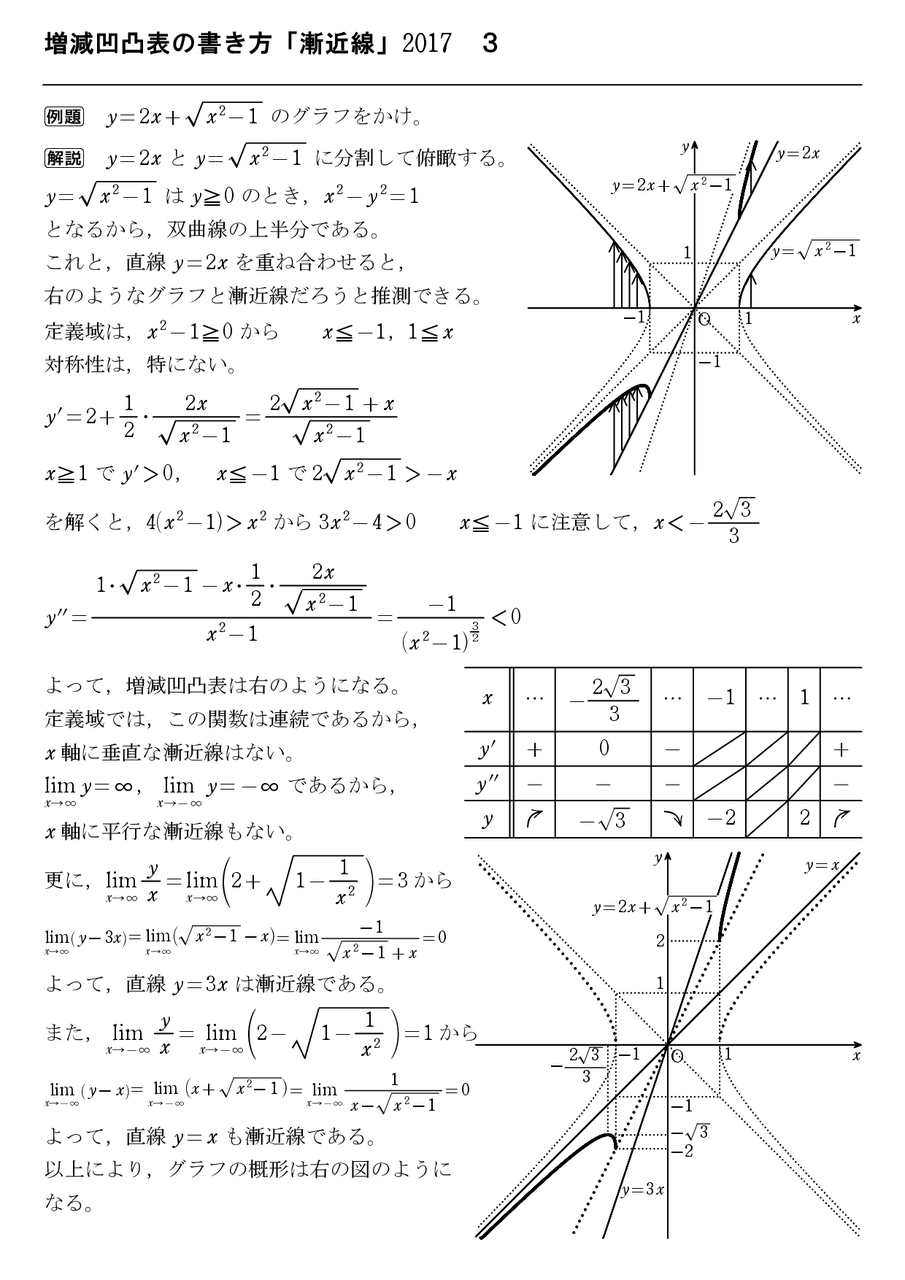


増減凹凸表の書き方 漸近線 17 3 怜悧玲瓏 高校数学を天空から俯瞰する



漸近線の求め方が分かりません 3 です Clear



数 微分法 漸近線 縦線タイプ オンライン無料塾 ターンナップ Youtube
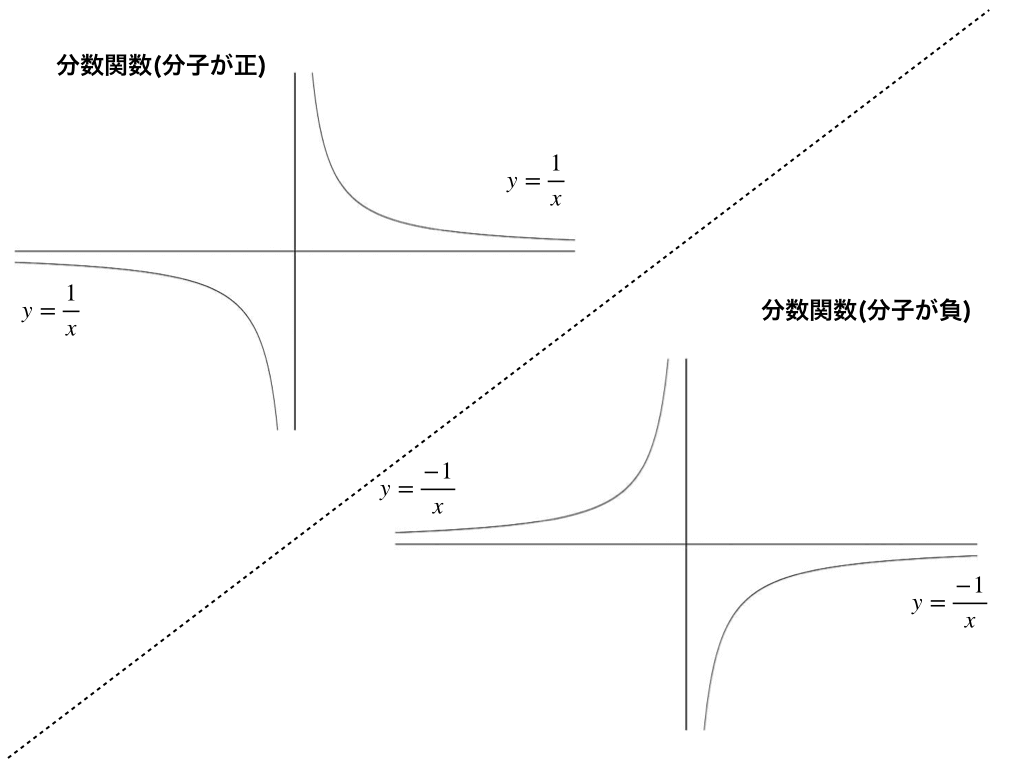


分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法
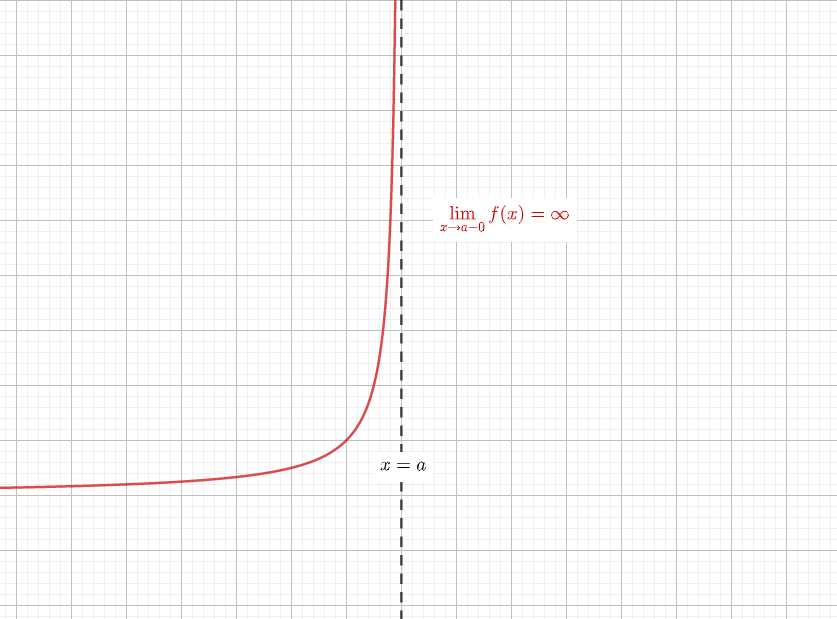


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



漸近線とは 求め方 高校数学 Youtube



数学3編 完全攻略 高校数学の公式全部まとめてみたwww Cupuasu クプアス



数3の微分の応用のところの漸近線の求め方がわかりません Clear


Studydoctor漸近線とは 求め方 高校数学 Studydoctor



高校数学 グラフのかき方 2 問題編 映像授業のtry It トライイット



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学塾



数3 関数の極限 グラフ 漸近線 高校数学に関する質問 勉強質問サイト


高校数学 分数関数のポイント整理 双曲線と漸近線 偏差値40プログラマー


011 7 49 大学受験完全個別指導予備校 実力養成会 The Ability Training School 実力養成会について 学習システム 費用 ニュース ブログ 実力養成会を選んだ理由 実力養成会の考え方 講師紹介 実績 よくあるご質問 ニュース ブログ ホーム ニュース



漸近線の方程式がy 2x 5 Y 2x 3で 点 1 1 を通る双曲線の方程式を その他 教育 科学 学問 教えて Goo



Mks ん いまいちわかんねえ 124 1 の漸近線のところで詰まってる Y X 2の方 は解説貰ってるからなんとかなるんだが Lim X 2 0 Yの具体的な求め方がわからん



漸近線の描き方 一目瞭然早見チャート 高校生 数学のノート Clear



分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法



漸近線 Wikiwand



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学塾



曲線を無限に遠ざけた時に漸近線に近づいていくという事 高校数学に関する質問 勉強質問サイト



数3 高校数学に関する質問 勉強質問サイト
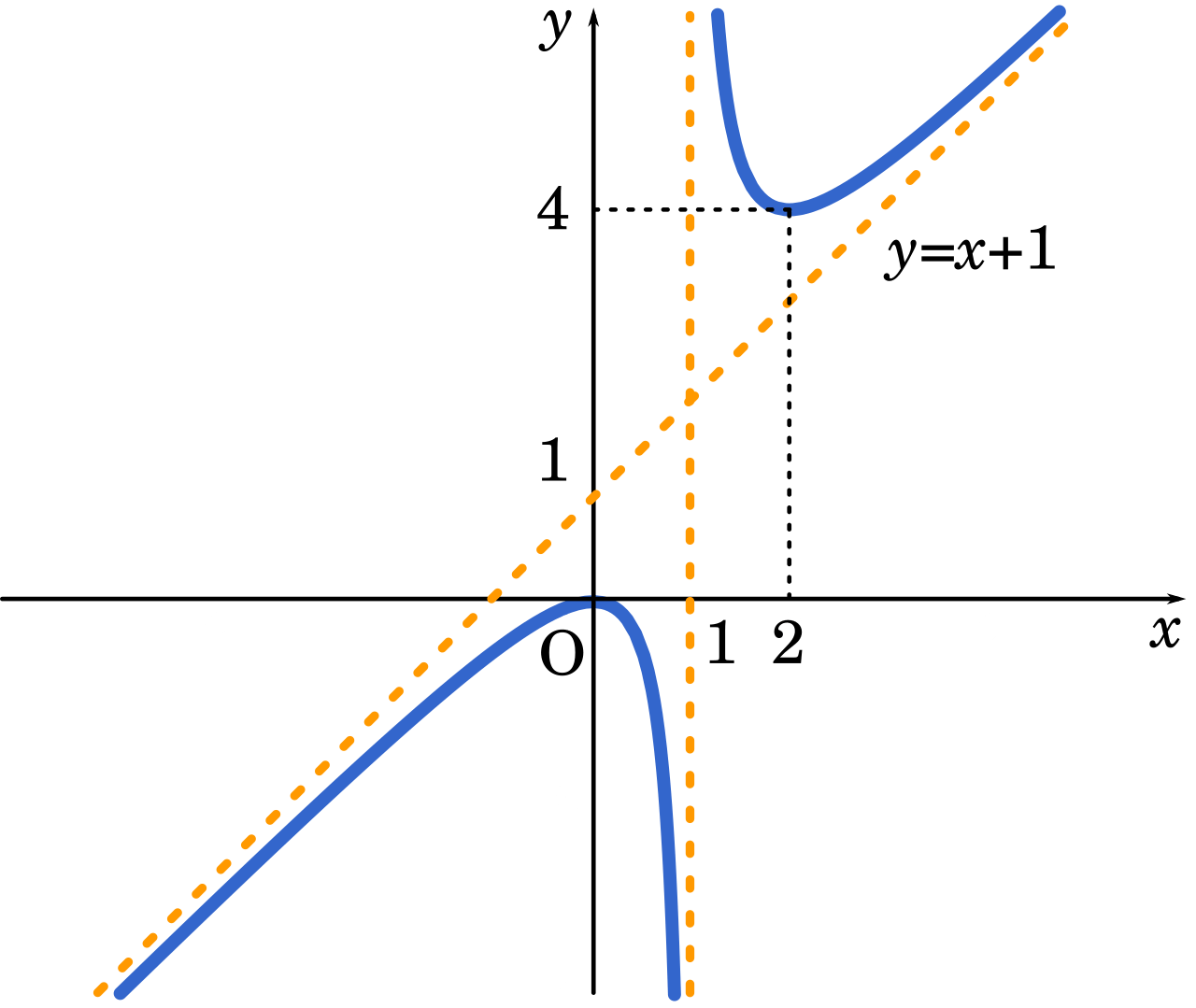


数 微分の応用 ざっくりイメージから漸近線を導く Mm参考書



双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ
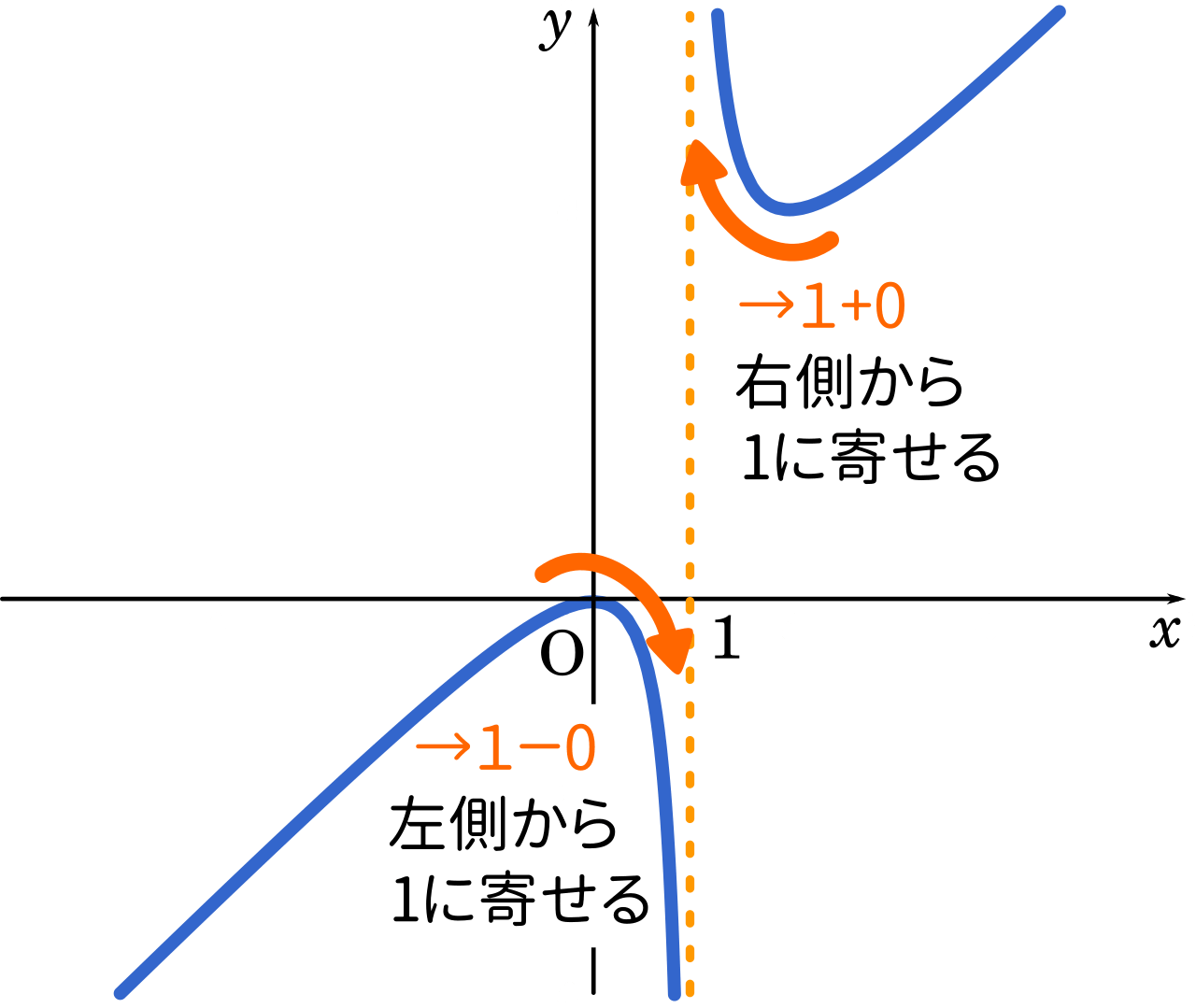


数 微分の応用 ざっくりイメージから漸近線を導く Mm参考書



この漸近線の求め方がわかりません なぜy Xをするのか教えて下さい Clear


どうして 中心が原点 漸近線の傾きが 2で 点 1 2 0 を通 Yahoo 知恵袋


高校数学の数3の漸近線の求め方なのですが なぜ括弧の中のような事 Yahoo 知恵袋
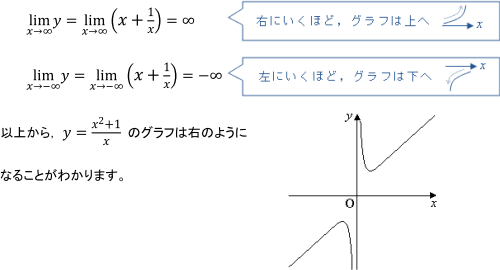


複雑な関数のグラフのかき方 数学 苦手解決q A 進研ゼミ高校講座



対数関数の漸近線の求め方がわかりません ス せ ソの解説をお願いしたいです Clear


漸近線の求め方3パターン 具体例で学ぶ数学



漸近線の求め方を解説しました 無料解説 数学の勉強が一人でできる 医学部受験応援サイト


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



漸近線の求めかた Y X 1 1 X 1 のグラフを描く問題なんですが 数学 教えて Goo



双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ



数3 なるべく早く回答求む 高校数学に関する質問 勉強質問サイト



基本 双曲線と漸近線 なかけんの数学ノート



高校数学 分数関数のグラフ 1 映像授業のtry It トライイット



漸近線 Wikipedia


数3グラフの概形を書くときに漸近線を調べると思うんですが どこを調べれば Yahoo 知恵袋



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学塾
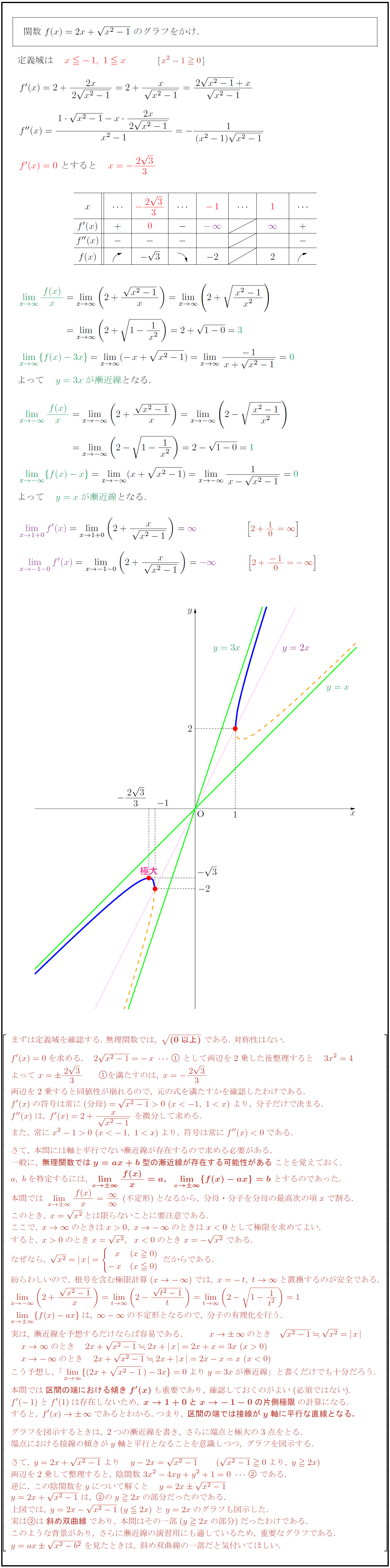


高校数学 無理関数 Y 2x X 1 のグラフ 斜め双曲線 受験の月


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック
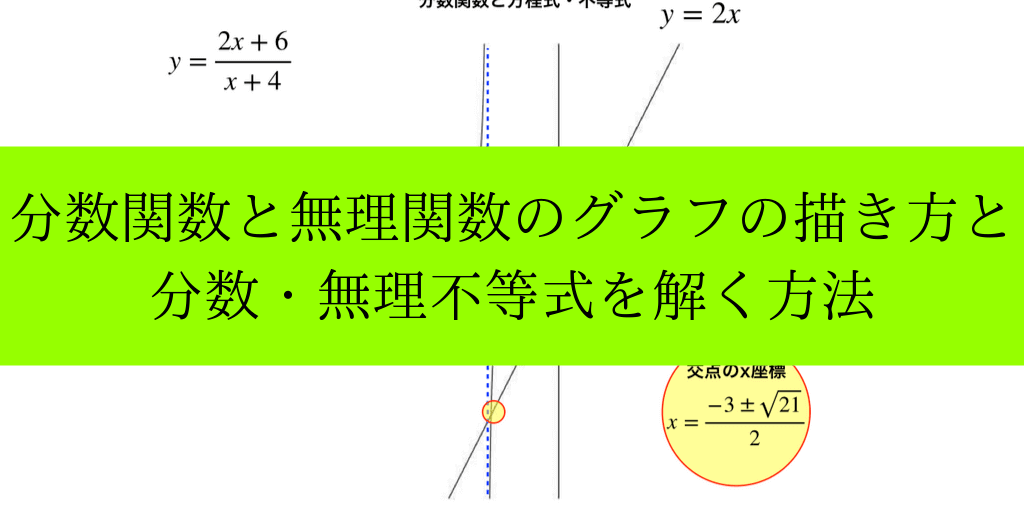


分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法



漸近線の求め方 高校数学 微分法の応用 15 Youtube



標準 微分と関数のグラフと漸近線 なかけんの数学ノート



数学についてです 数iiiのグラフの問題で グラフの概形を描くために 数学 教えて Goo


数 の関数のグラフで 漸近線の求め方が全然わかりません チャート読んで Yahoo 知恵袋



三角関数のグラフの書き方とコツ Sin Cos Tan 周期 理系ラボ



高校数学 双曲線のグラフ 1 映像授業のtry It トライイット
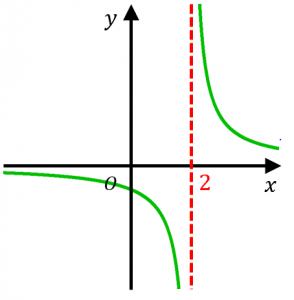


漸近線の求め方3パターン 具体例で学ぶ数学



一次分数関数のグラフと漸近線 高校数学の美しい物語
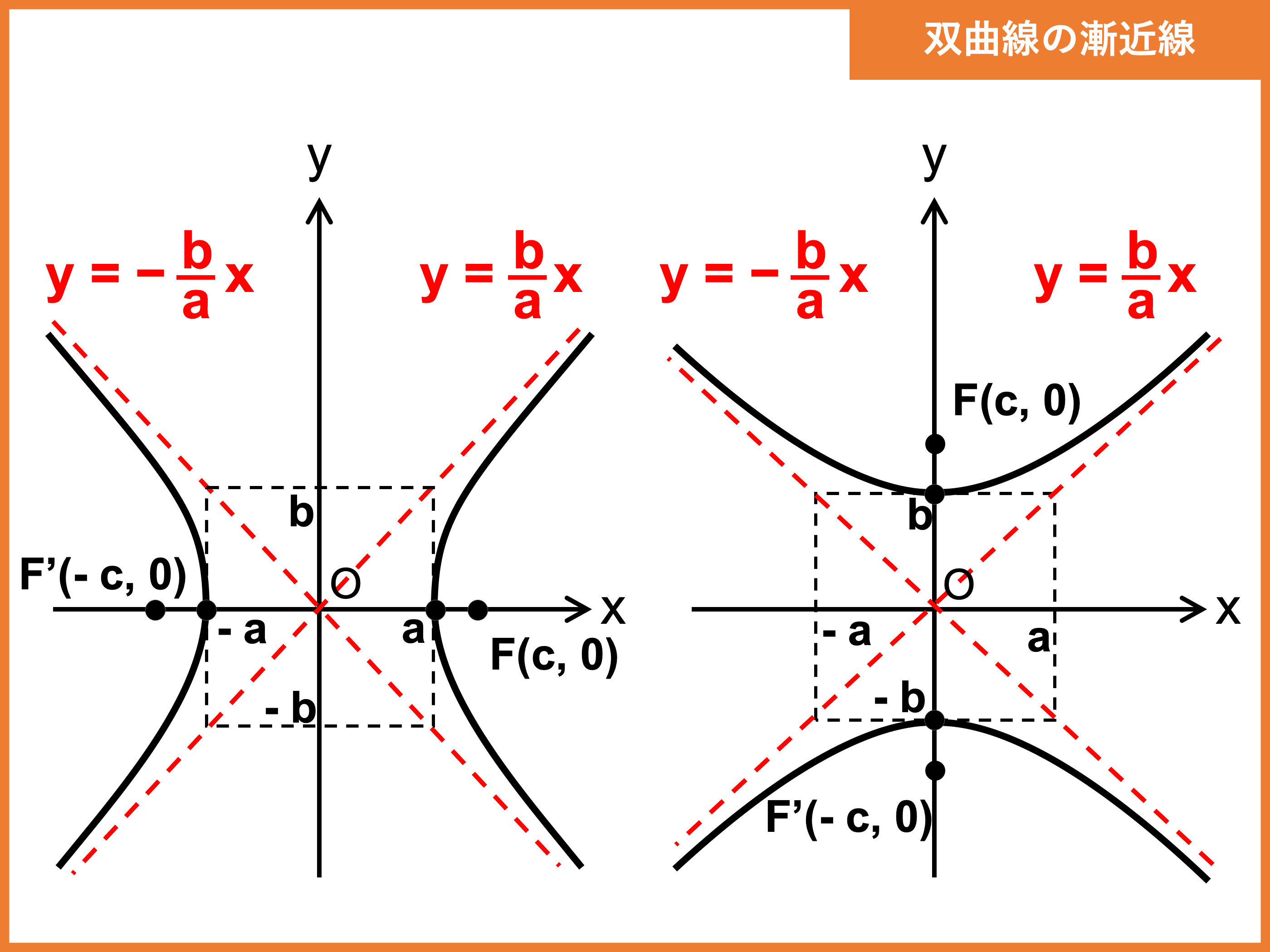


双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典



うさぎでもわかる線形代数 第21羽 2次形式の応用 2次曲線のグラフ 工業大学生ももやまのうさぎ塾



漸近線の求め方が分かりません 3 です Clear



タカタ先生のガチ授業 数 関数と極限 分数関数の漸近線の求め方 裏技 勉強 Youtube スタディチューブ



変曲点に関する質問 勉強質問サイト
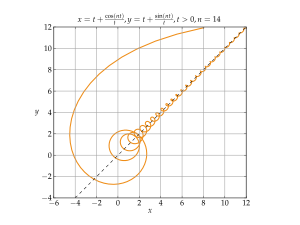


漸近線 Wikipedia
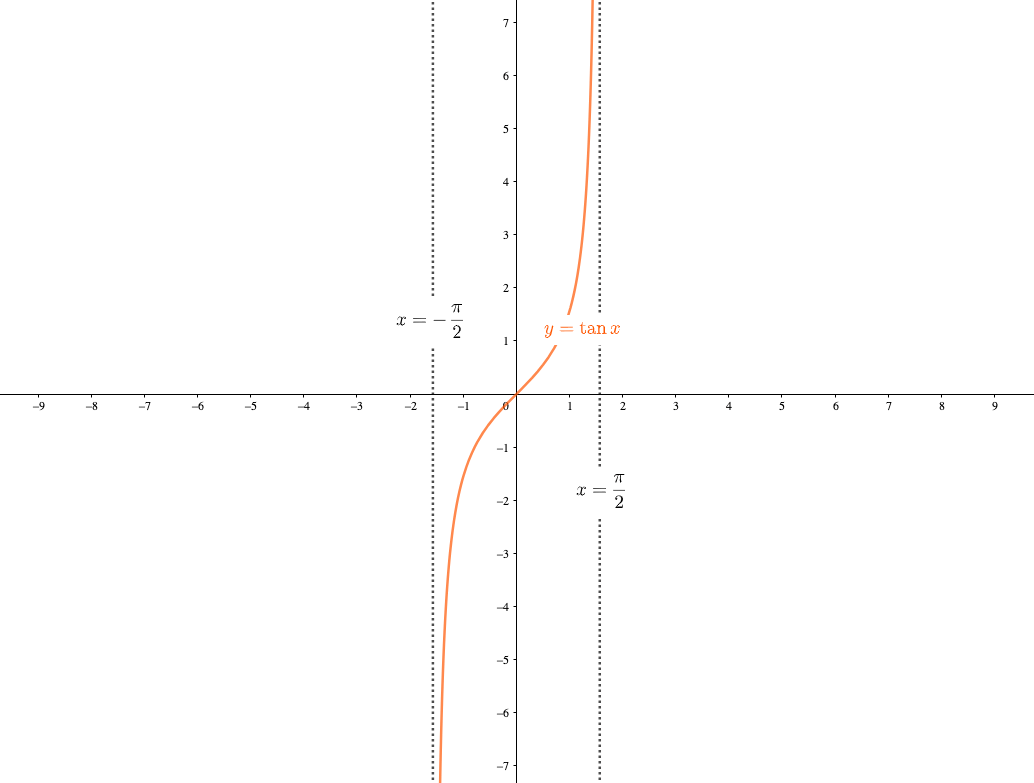


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



漸近線の求め方 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc


関数y X 2 X 1 の漸近線を求めよお願いします Llllh Yahoo 知恵袋
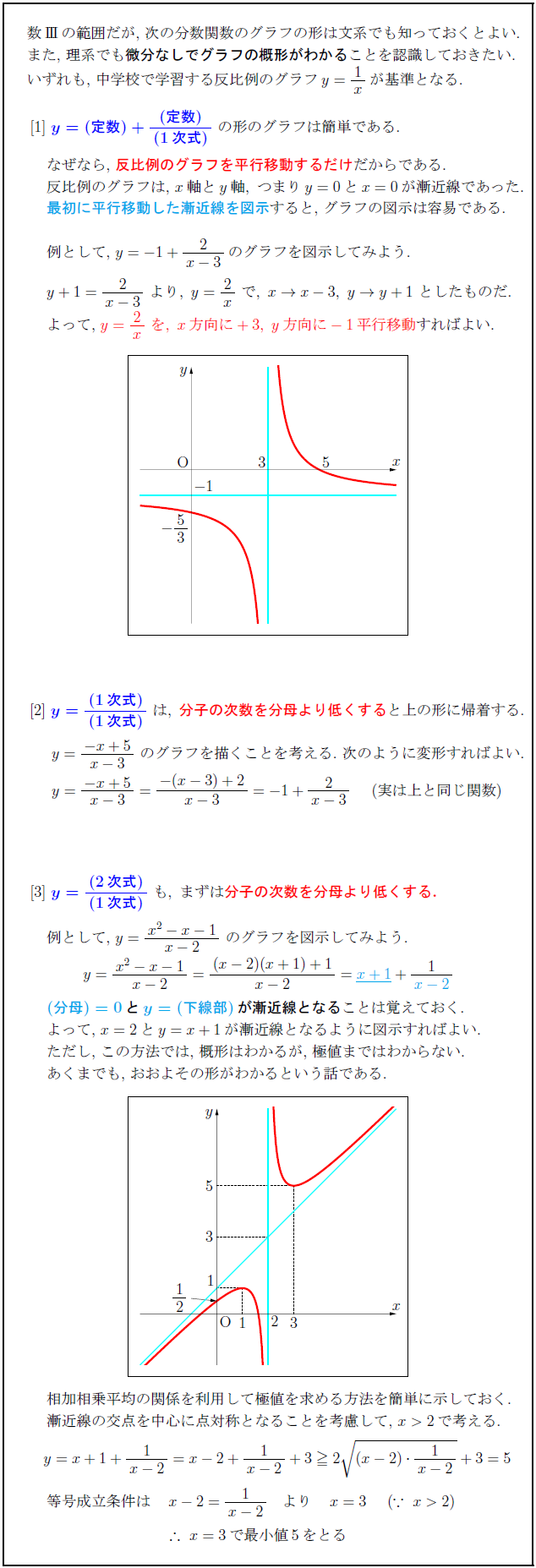


高校数学 文系も知っておくべき基本的な分数関数 数 のグラフ 受験の月
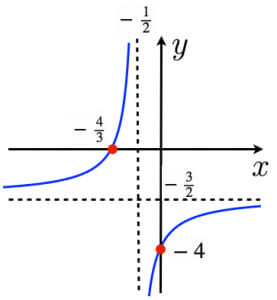


一次分数関数のグラフと漸近線 高校数学の美しい物語



数 標準問題精巧 高校数学に関する質問 勉強質問サイト



分数関数のグラフの書き方 定義域 漸近線 数学の偏差値を上げて合格を目指す


数 の関数のグラフで 漸近線の求め方が全然わかりません チャート読んで Yahoo 知恵袋


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック
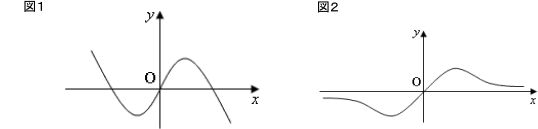


複雑な関数のグラフのかき方 数学 苦手解決q A 進研ゼミ高校講座



漸近線 Wikiwand
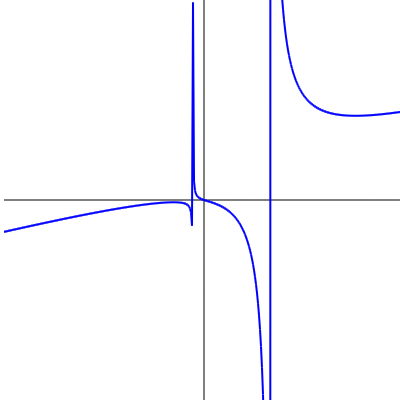


Javascript Y軸に平行な漸近線を描く Mm参考書
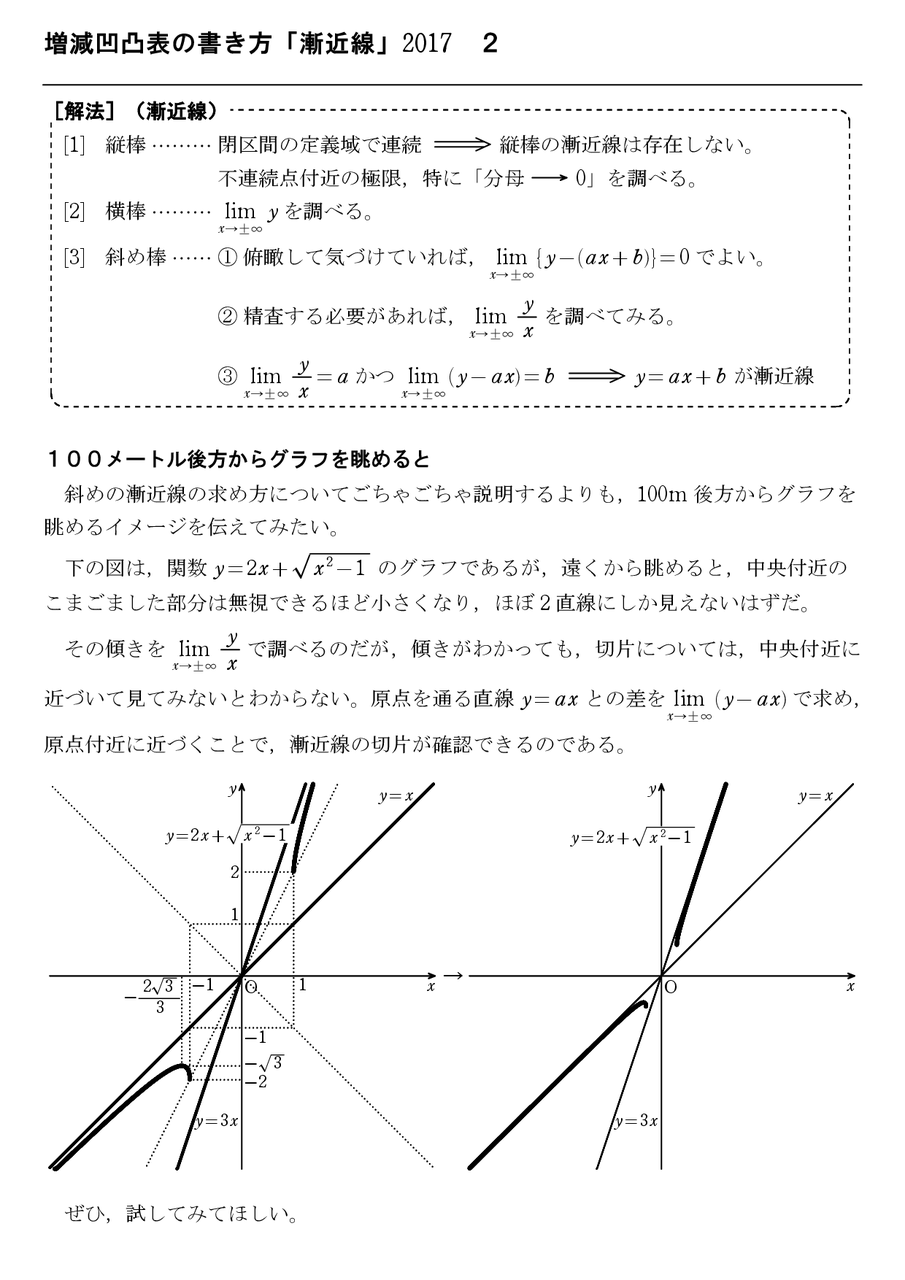


増減凹凸表の書き方 漸近線 17 2 怜悧玲瓏 高校数学を天空から俯瞰する



数 関数と極限 この問題 なんでy X 2が漸近線になると分かるんですか 数学 教えて Goo
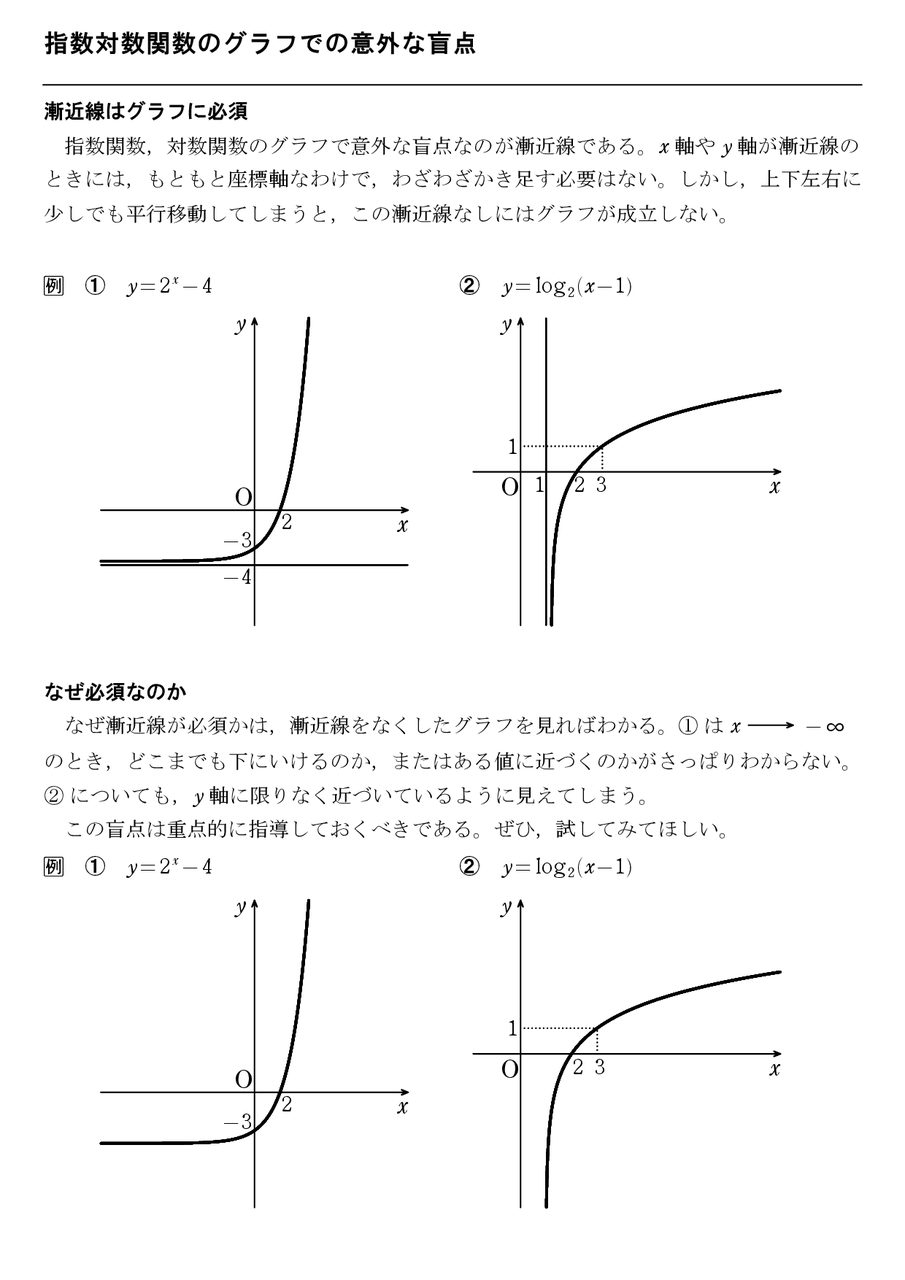


数学ii 怜悧玲瓏 高校数学を天空から俯瞰する


双曲線の方程式


漸近線の求め方についてなぜこのようなことが成り立つのか 教科書には説明が Yahoo 知恵袋



分数関数のグラフの書き方 定義域 漸近線 数学の偏差値を上げて合格を目指す
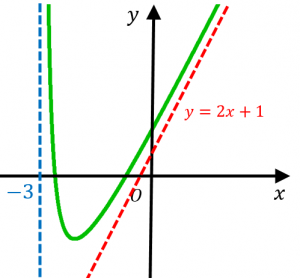


漸近線の求め方3パターン 具体例で学ぶ数学



双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ
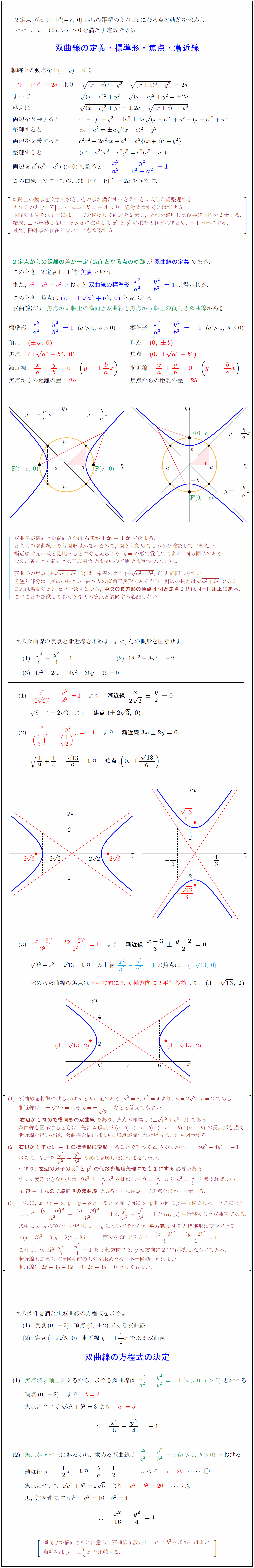


高校数学 双曲線の定義 標準形 焦点 漸近線 双曲線の方程式の決定 受験の月



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学塾


